Without knowing how a material reacts to tension, or how much of it it can take, your engineered products and structures can fail and leave you scratching your head. A great way to avoid this is via a stress-strain curve graph that provides a visual explainer of a material’s qualities and how it will respond to various stressors. We’ll explain exactly how the graph works and how you can read it in this article.
What is Stress?
There are many types of stress, but when it comes to the type engineers are working to discover, the simplest definition is the amount of force that gets applied to a cross-sectional area. Knowing this gives you an understanding of how much a material can handle before it fractures or breaks. The formula for figuring it out can be seen below:
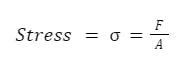
Stress formula.
- 𝜎 = stress
- F = applied force
- A = cross-sectional area
What is Strain?
Although stress and strain are often talked about together, the latter is the deformation a material goes through compared to its original dimensions. It’s another calculable reference point that’s essential for helping engineers really know a material better, and get the best idea of when a structure or item made of a specific material will break. Strain is an example of a unitless value (as both the numbers in the formula are lengths), and the formula looks like this:
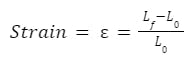
Strain formula.
- ε = strain
- Lf = final length after the deformation happens
- L0 = original or starting length
What is the Stress-Strain Curve?
Now we’re going to take a look at measuring the stress-strain curve and what kinds of information can be pulled from it. In manufacturing today, there are many machines that do all the measuring for you. These curves usually are created by a modern tensile testing machine, and the said graphs are standardized through ASTM International under a few categories—E8 for metals and D638 for plastics. You can expect tests and measurements to create this curve to go something like this:
- You or the operator will source or create a test material with the right dimensions.
- Then you’ll clip or attach the test material to the jaws of the testing machine.
- The machine will then place a tensile load onto the material and increase that load until the material breaks.
- Once this happens, the machine will note the stress and strain values based on those readings.
Stages and Regions of the Curve
Once you have a graph showing the stress-strain curve, it’s worth understanding the regions, stages, and information you can parse from it. The three stages are elastic deformation, uniform deformation, and necking. Elastic deformation is when a material experiences stress but can still snap back to its original dimensions. Uniform deformation happens for as long as a material can handle strengthening through strain hardening—which is a show of its brittleness or ductility. Necking is when the ultimate tensile strength has been reached and strain hardening isn’t possible anymore. Localized deformation will appear somewhere in the material’s cross-section, its dimensions decrease while stress increases, and then it’s past the point of no return and deforms or breaks permanently.
Now that you know the stages, you can understand the regions and pick out five of the most important points on the graph, which we’ve briefly described below:
- Proportional limit: The end point of the linear portion on the stress-strain curve which Young’s modulus can be pulled from by calculating the slope.
- Elastic Limit: The end point for elastic deformation, which is then taken over by plastic deformation (it’s hard to distinguish it from the elastic limit when you’re measuring metals).
- Yield Point: The same as the elastic limit, but calculable, so much more reliable for engineers. To work it out, offset the linear portion of the curve by +0.2% along the horizontal axis. Then, you find the intersection point between the offset line and the original stress-strain curve, and you have the yield strength.
- Ultimate Stress Point: The highest amount of stress on the stress-strain curve, after which necking starts. It’s also important to note that while this is the highest on the graph, the actual highest point happens right when the material breaks.
- Fracture or Breaking Point: As its name says, this is the point on the curve where your material has deformed so much it has finally broken or fractured.
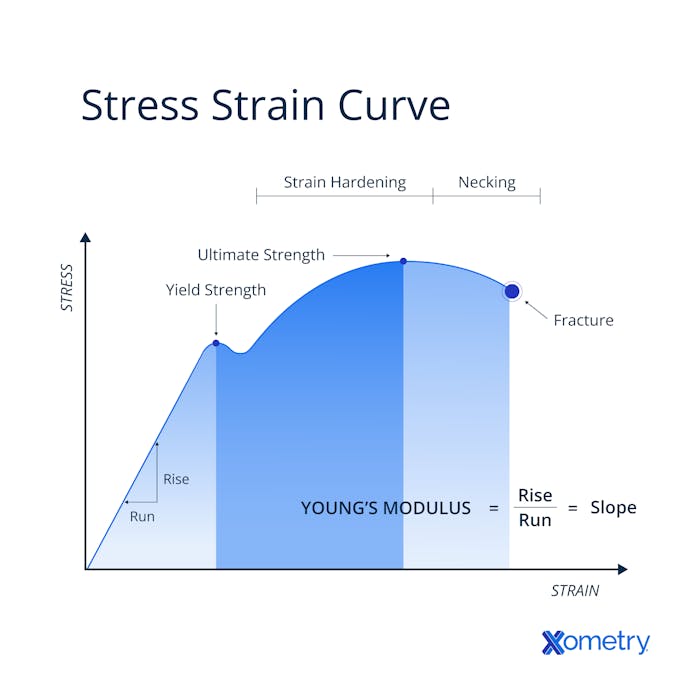
How to Read the Graph
Here’s a quick guide to reading one of these graphs:
- Choose a stress value on the Y-axis.
- Draw a horizontal line from the Y-axis until it intersects with the line of the stress-strain curve. Make a dot on that point.
- Draw a vertical line from the intersection point to the X-axis. Together, these lines should form a 90-degree angle.
- The stress value you picked in step one shows the stress that corresponds to the deformation (or strain) that happens to the material at that point.
Stress and Strain Types
There are two types you’ll find on the stress-strain curve, engineering stress and strain, and true stress and strain.
Engineering Stress and Strain
The first type (engineering) is also called nominal stress and strain and is calculated without considering the very small details of plastic deformation. It’s an easy way to get values through a standard tensile test and understand the performance of a material. The formula for engineering stress looks like this:
Engineering stress formula.
A0 stands for the original cross-sectional area of your test material, and both the Pascal (Pa) and pounds per square inch (psi) are used as units. The formula for engineering strain looks like the following and is a unitless measurement:

Engineering strain formula.
True Stress and Strain
This is the actual stress and strain value you get if you take plastic deformation into account. Doing calculations for this specific type of stress and strain is great for learning the mechanical properties of a material, and to find it you need to use experimental data on the instantaneous gauge length, cross-sectional area, and applied load. The formula for finding true stress looks like this:
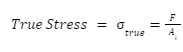
True stress formula.
Ai stands for the instantaneous cross-sectional area. To then find the true strain, use the formula below, where Li stands for instantaneous length:
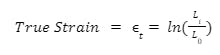
True strain formula.
How Xometry Can Help
We at Xometry work with many different materials that are important to engineers and manufacturers and can offer free quotes for everything from CNC machining to 3D printing to sheet laser cutting.
Disclaimer
The content appearing on this webpage is for informational purposes only. Xometry makes no representation or warranty of any kind, be it expressed or implied, as to the accuracy, completeness, or validity of the information. Any performance parameters, geometric tolerances, specific design features, quality and types of materials, or processes should not be inferred to represent what will be delivered by third-party suppliers or manufacturers through Xometry’s network. Buyers seeking quotes for parts are responsible for defining the specific requirements for those parts. Please refer to our terms and conditions for more information.


