Elastic modulus, also known as the modulus of elasticity, is a significant mechanical property that describes a material’s stiffness. Calculating a material’s elastic modulus helps engineers determine the material’s ability to retain its shape when a load is applied and is fundamental to designing safe structures.
There are four types of elastic modulus. Each is associated with a different type of deformation. It is important for engineers to refer to the correct elastic modulus value when designing parts or structures for a particular application.
Elastic modulus can be determined mathematically from Hooke’s law, which describes the relationship between force and the displacement experienced by a spring.
Specifically, Hooke’s Law states, "the force exerted by a spring is directly proportional to the displacement of the spring from its equilibrium position, provided the limit of elasticity is not exceeded."
After the elastic limit is reached, the spring will not return to its exact initial state.
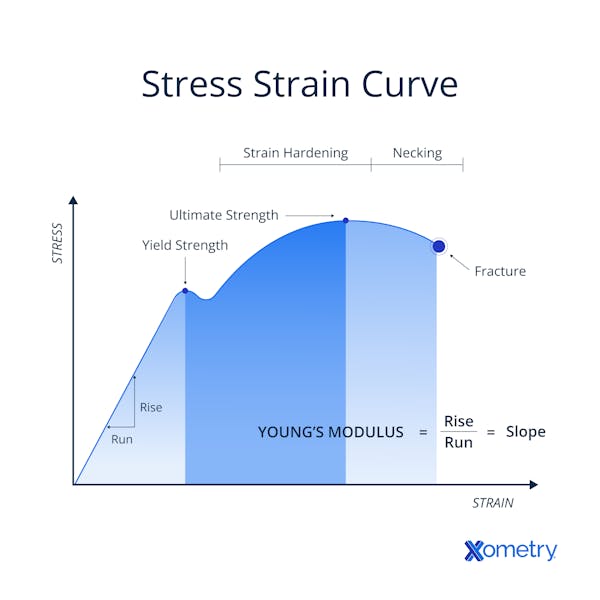
Elastic modulus can be thought of as a form of Hooke’s Law since elastic materials act similarly to springs in the elastic region of the stress-strain curve. The elastic region on a stress-strain curve is generally linear until the elastic limit is exceeded.
Like stress, the modulus of elasticity is reported as a force per unit area and is often shown in gigapascals (GPa) or pounds per square inch (psi). This article will review the five main steps in calculating elastic modulus and provide a brief overview of its significance and meaning.
1. Choose a Testing Method
The first step in calculating the elastic modulus is to determine what type of elastic modulus information is needed for the particular application. Each modulus gives insight into how a material behaves when subjected to a different type of loading.
- Young’s modulus describes elasticity under tensile and compressive loads.
- Shear modulus, on the other hand, describes elasticity in conditions of shear stress.
- Bulk modulus refers to elasticity in all directions.
- Finally, flexural modulus is related to elasticity in bending.
The test procedure for determining the modulus of elasticity follows similar principles to those for determining material strength, but it specifically measures deformation within the elastic region of a stress-strain curve. The appropriate procedure for the desired stress conditions (tensile, compressive, shear, flexural, hydrostatic) should be followed as defined in the relevant ASTM standard. There are numerous ASTM standards for the determination of the various elastic moduli, and each standard is intended for use with a particular material.
For example, a common ASTM standard for the determination of Young’s modulus (tensile modulus) in plastics is ASTM D638 (Standard Test Method for Tensile Properties of Plastics).
ASTM E8/E8M is the Standard Test Method for Tension Testing of Metallic Materials.
ASTM D3039 is the Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials.
You will notice that these standards do not explicitly mention “elastic modulus” in the standard name or description. This is because these standards are primarily for standardized strength tests, and the elastic modulus is calculated using the data obtained from a strength test (it is not measured directly).
2. Perform the Experiment
Once the test specimen is prepared, a universal testing machine (UTM) or materials testing system is used to apply a controlled load. This machine continuously records the applied force (load) and the resulting displacement (deformation) in the gauge section of the specimen. For tensile tests, the sample is loaded until it fractures.
Using this data, stress and strain are calculated, which are then used to determine the elastic modulus from the linear portion of the stress-strain curve.
3. Calculate Stress
During testing, many materials testing systems automatically generate a stress-strain curve.
Stress (σ) is calculated as:
𝜎=𝐹/𝐴0
where:
𝐹 = applied force (load)
𝐴0 = original cross-sectional area of the specimen
If a stress-strain curve is available, stress values can be directly obtained from the plotted data. Otherwise, stress must be calculated manually using the applied load and initial cross-sectional area.
4. Calculate Strain
As with stress, many materials testing systems will automatically record and graph strain on the X-axis of a stress-strain curve. From this curve, strain values at different loading stages can be directly obtained.
However, if a stress-strain curve is not available, strain must be calculated manually. Strain is defined as the ratio of the change in length of a material to its original length.
It is calculated using the formula:
𝜀 = Δ𝐿/𝐿0
where:
ε = strain (dimensionless, often expressed as a percentage)
ΔL = change in gauge length (elongation or compression)
𝐿0 = original gauge length
For more information, see our guide on How to Calculate Strain.
5. Calculate the Elastic Modulus
The elastic modulus is the slope of the straight-line elastic (recoverable strain) part of the stress-strain curve traced out by the testing machine. Modern equipment will determine the slope and report it automatically. If the modulus has to be calculated, the simplest method is to simply select two points that are on the linear part of the slope and calculate the slope (rise-over-run) from stress divided by strain. It is customary to use a statistical method such as least-squares fit to make sure that only the straight part of the stress-strain curve is used in the calculation. Elastic modulus has the same units as stress since strain is a unitless value. Once the elastic modulus is obtained, engineers have more insight into how the material will behave when different types of loads are applied.
What Is the Importance of Calculating Elastic Modulus?
Elastic modulus describes how stiff a material is. Knowing a material’s stiffness, along with knowledge of the material’s yield strength enables one to calculate how much stress can be applied without permanent deformation.
To accommodate the calculated stresses, a material with a high enough modulus should be selected. Otherwise, the geometry of the part (larger cross-section, for example) can be changed to accommodate the anticipated stress while experiencing only elastic deformation. Limiting deformation to the elastic region will improve a material’s durability and provide a safety margin of performance to avoid the risk of catastrophic failure and potential harm to people and property.
What Is the Formula for Elastic Modulus?
The formula for elastic modulus is derived from Hooke’s law. The formula for elastic modulus is an extension of Hooke’s law to materials, where stress, elastic modulus, and strain replace force, spring constant, and displacement, respectively. By solving for elastic modulus, it can be shown that elastic modulus is equal to the ratio of stress-to-strain. The formula for elastic modulus, as derived from Hooke’s law, is shown below:
E=𝝈/ε
Where:
E= Elastic modulus (Pa or psi)
𝝈 = stress (Pa or psi)
ε = strain (unitless)
The equation above is for tensile/compressive modulus. Stress (𝝈) is the force per unit area applied perpendicularly to the cross-section of interest, and ε is the change in length along the direction of applied stress.
These quantities are the stress and strain experienced in a uniaxial tensile test. If testing for other types of modulus, 𝝈 and ε are replaced by the appropriate type of stress and strain, respectively.
For example, to calculate shear modulus, the shear stress and shear strain are used. Table 1 below shows the symbols that pertain to each variable for each type of modulus. Table 1: Symbols and Equation for Each Type of Modulus
The flexural modulus equation differs from the equations for the other modulus types due to the elastic beam theory.
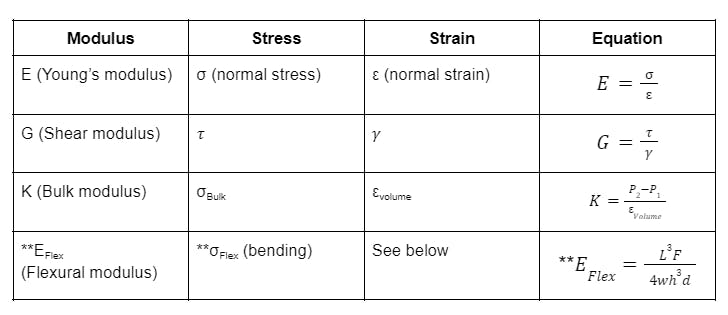
Table 1: Symbols and Equation for Each Type of Modulus
What Are the Different Types of Elastic Moduli?
There are four different elastic modulus values. Each describes the behavior of a material under different loading conditions. The four types of elastic moduli are listed and described below:
- Young’s Modulus: Young’s modulus describes the ability of a material to withstand deformation when subjected to uniaxial tensile or compressive loads.
- Shear Modulus: Shear modulus describes the ability of a material to resist shear deformation. Shear deformation occurs when shear loads (loads parallel to the cross-sectional area) are applied to a material.
- Bulk Modulus: Bulk modulus characterizes a material’s ability to withstand deformation when subjected to triaxial or isostatic loads.
- Flexural Modulus: Flexural modulus characterizes a material’s ability to withstand deformation due to bending loads.
How Are the Values of Elastic Modulus Expressed?
Elastic modulus is expressed in the same units as stress or applied force per unit area.
The SI unit for elastic modulus is Pascals (Pa), but for engineering materials, the elastic modulus is quite high and is typically shown in megapascals (MPa) or gigapascals (GPa). In English / Imperial units, pounds per square inch (psi) or kilo pounds per square inch (ksi) are used.
What Material Has the Highest Elastic Modulus?
Diamond is one of the stiffest known materials, with Young’s modulus of approximately 1,220 GPa. That’s more than twice as high as metals like tungsten, rhenium, and osmium, which rank among the stiffest metals with values around 400–420 GPa. Certain engineered materials, such as aggregated diamond nanorods, are stiffer than natural diamond.
What Does a Large Elastic Modulus Value Indicate?
A large elastic modulus denotes that a material is highly resistant to elastic deformation and, therefore, highly rigid. For a given level of applied stress, a material with a high elastic modulus will deform less than a material with a low modulus. Consider a material that is subjected to a stress of 100 MPa. If the material’s elastic modulus is 10 GPa, the applied stress will result in a strain (elastic deformation) of 0.01, whereas if the modulus is 100 GPa, the strain will only be 0.001. The higher value of modulus results in less deformation.
What Does a Small Elastic Modulus Value Indicate?
A smaller elastic modulus denotes that a material is more susceptible to elastic deformation and, therefore, more flexible. Consider a material where a stress of 100 MPa is applied. If the material’s elastic modulus is 10 GPa, the applied stress will result in a strain (elastic deformation) of 0.01, whereas if the modulus is 1 GPa, the strain will be 0.1. The lower value of modulus results in more deformation.
What Is the Elastic Modulus Symbol?
The capital letter “E” is often used to denote a material’s elastic modulus and refers to Young’s modulus. The capital letter “G” refers to the shear modulus, while the capital letter “K” refers to the bulk modulus. EFlex refers to the flexural modulus.
Are Stress and Strain Both Necessary for Calculation of Elastic Modulus?
Yes, both stress and strain are necessary for the determination of elastic modulus. This is because each type of elastic modulus value is defined as the ratio of stress to a strain given a particular set of loading conditions. For more information, see our guide on the Material Stress-Strain Curve.
What Is the Difference Between Elastic Modulus and Shear Modulus?
Elastic modulus is a general term that refers to a material’s ability to withstand elastic deformation. If not otherwise specified, elastic modulus refers to a material’s ability to withstand elastic deformation when uniaxial tensile or compressive loads are applied (a.k.a Young’s Modulus).
Shear modulus is a type of elastic modulus that specifically quantifies a material’s ability to resist shear deformation. Shear deformation occurs in a direction parallel to the cross-sectional area at which shear stress is applied. For more information, see our What is Shear's Modulus?
How Xometry Can Help
Xometry provides a wide range of manufacturing capabilities, including casting and other value-added services for all of your prototyping and production needs. Visit our website to learn more or to request a free quote.
Disclaimer
The content appearing on this webpage is for informational purposes only. Xometry makes no representation or warranty of any kind, be it expressed or implied, as to the accuracy, completeness, or validity of the information. Any performance parameters, geometric tolerances, specific design features, quality and types of materials, or processes should not be inferred to represent what will be delivered by third-party suppliers or manufacturers through Xometry’s network. Buyers seeking quotes for parts are responsible for defining the specific requirements for those parts. Please refer to our terms and conditions for more information.